| MaxiMath |
|
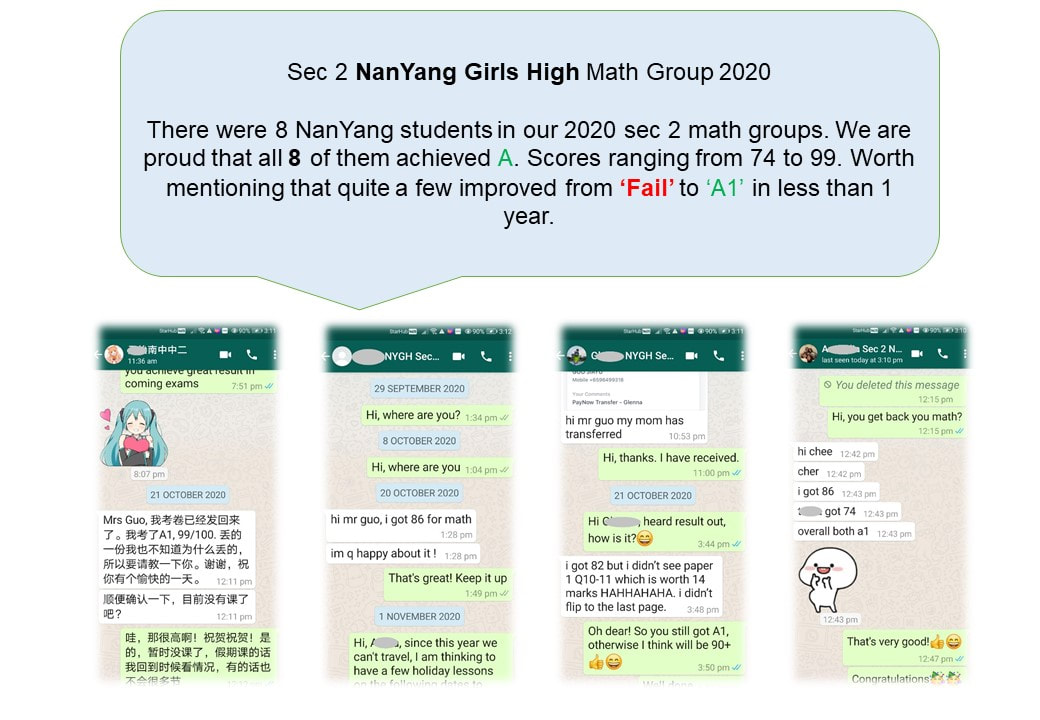
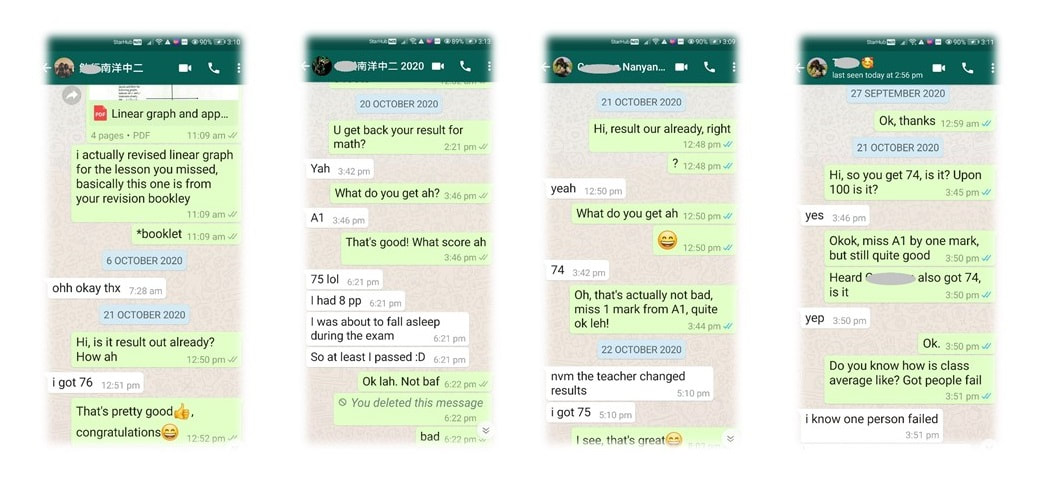
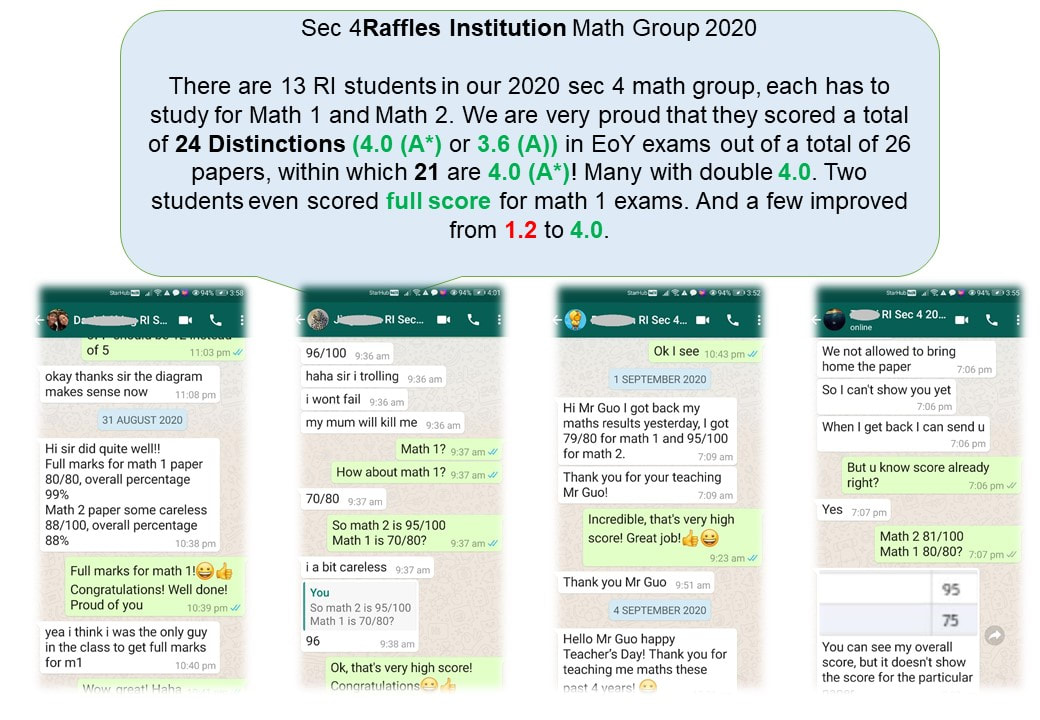
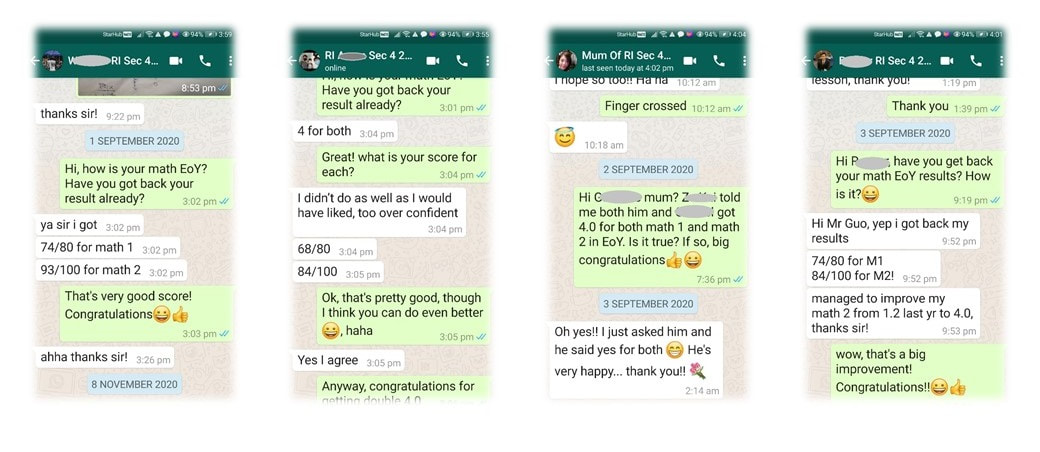
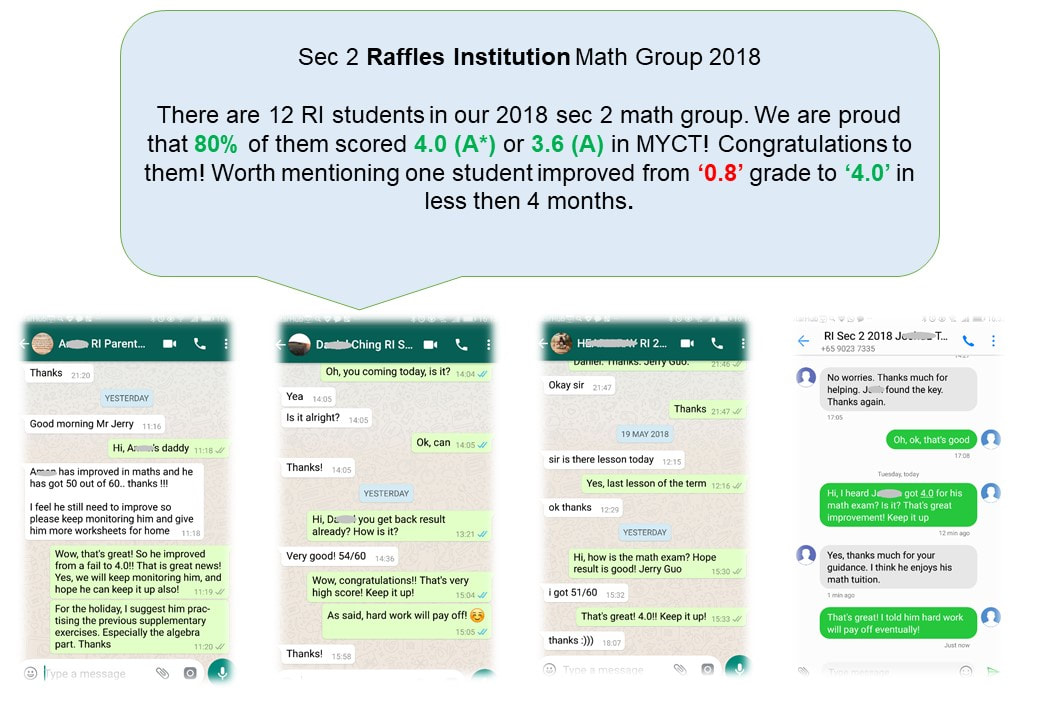
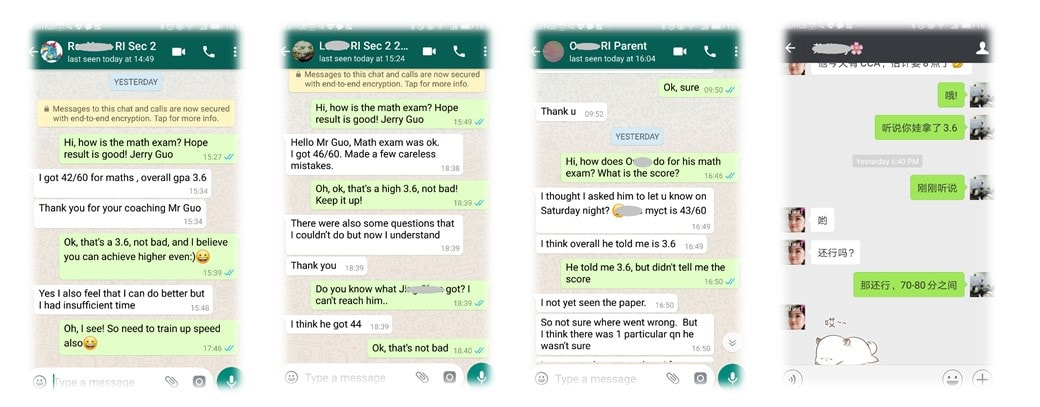
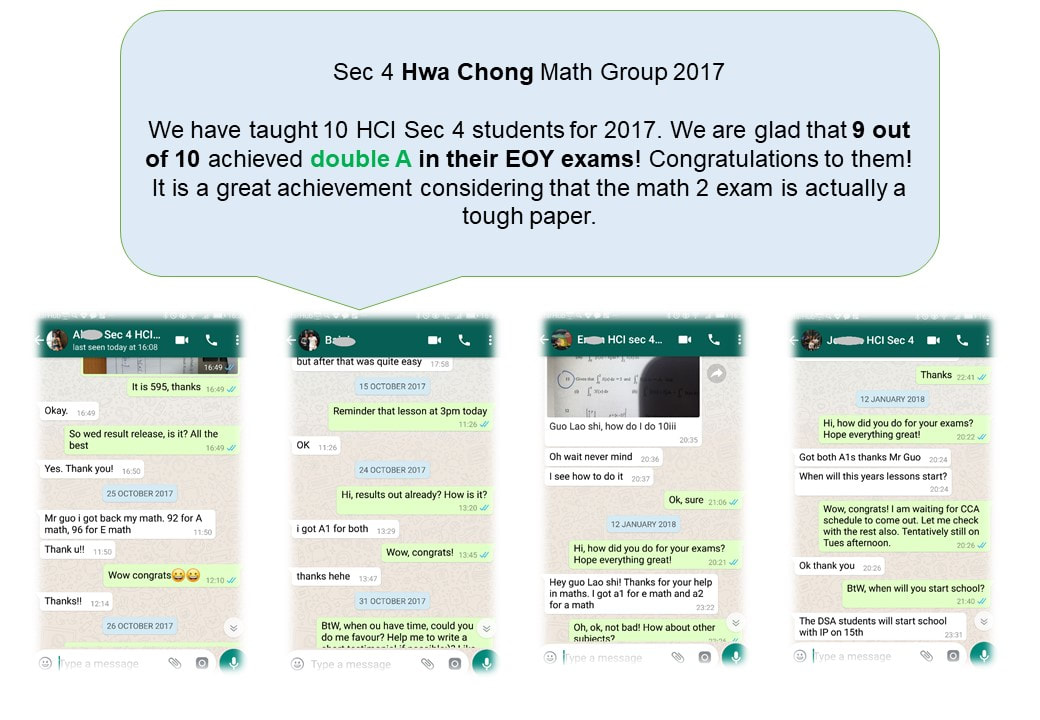
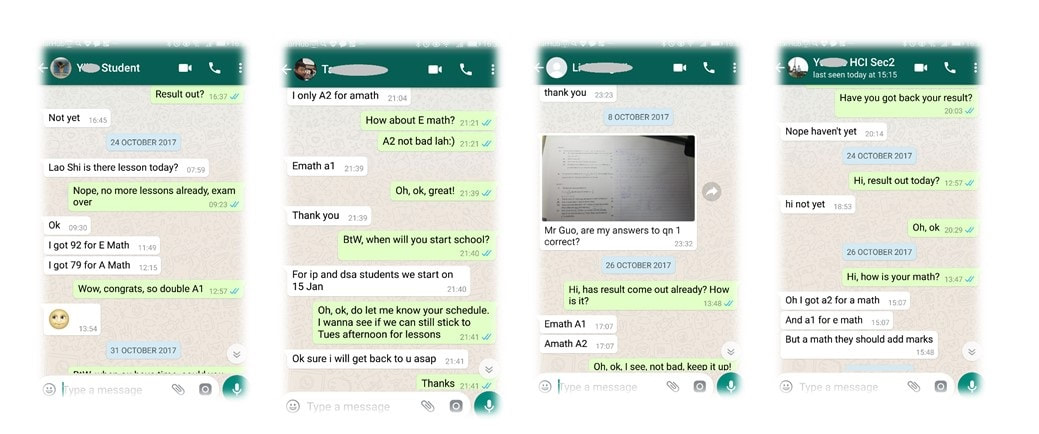
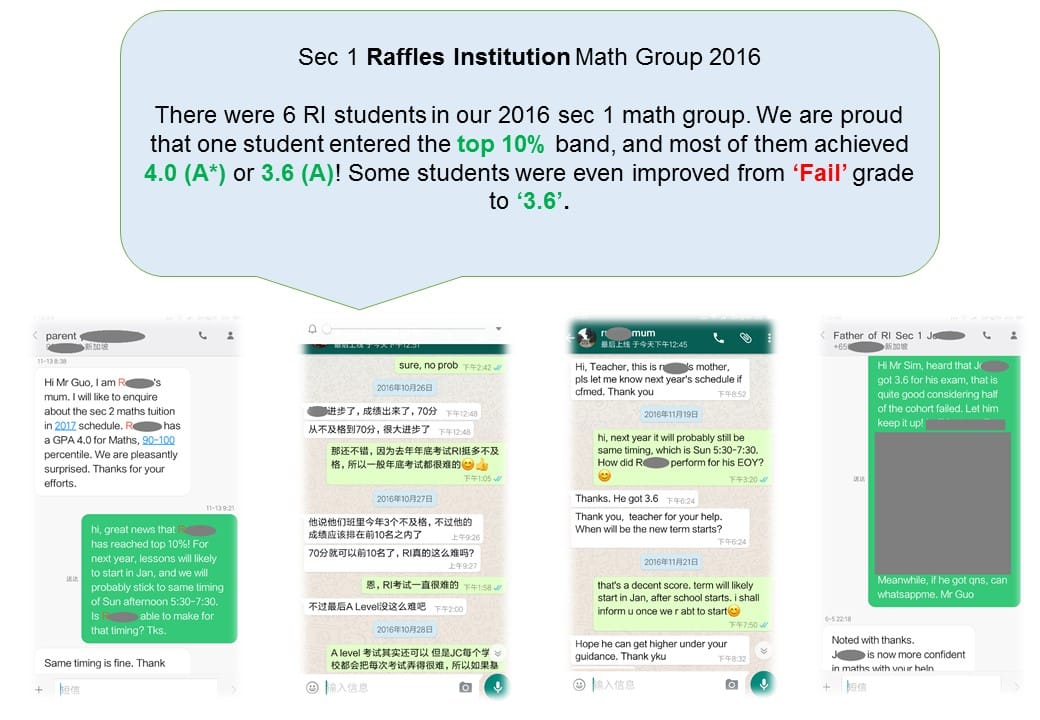
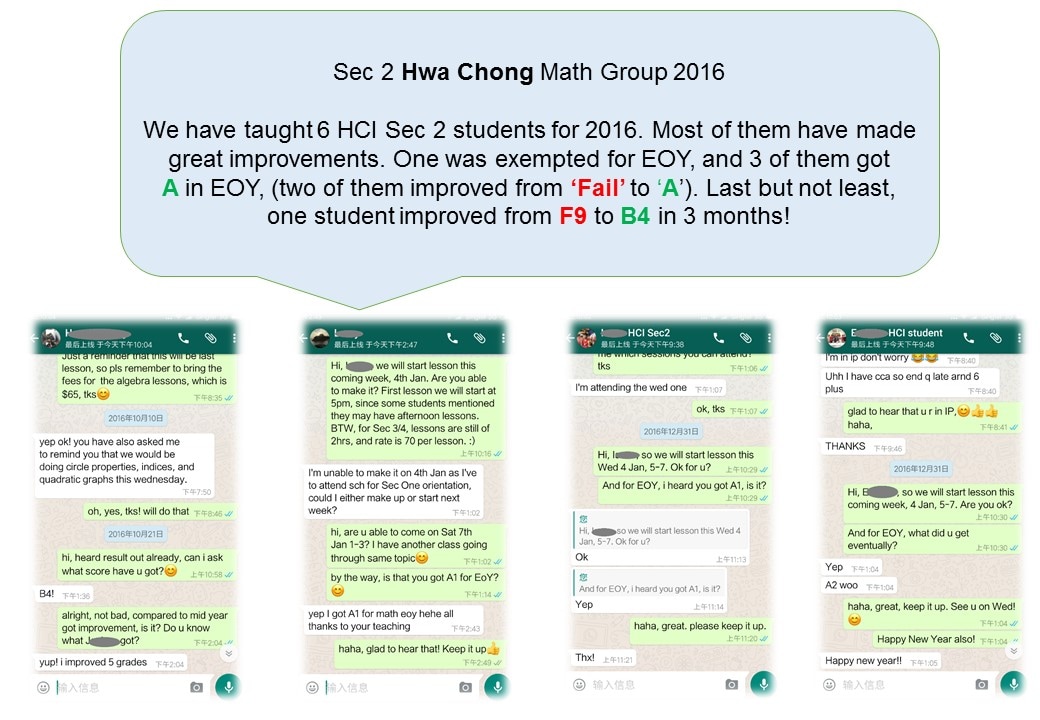
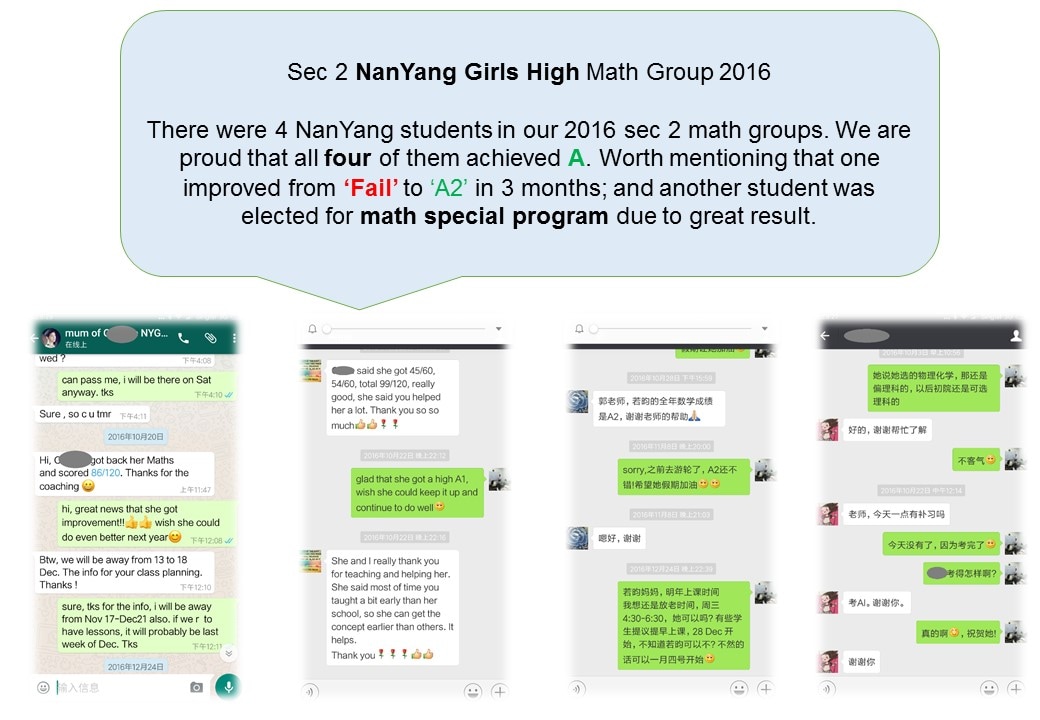
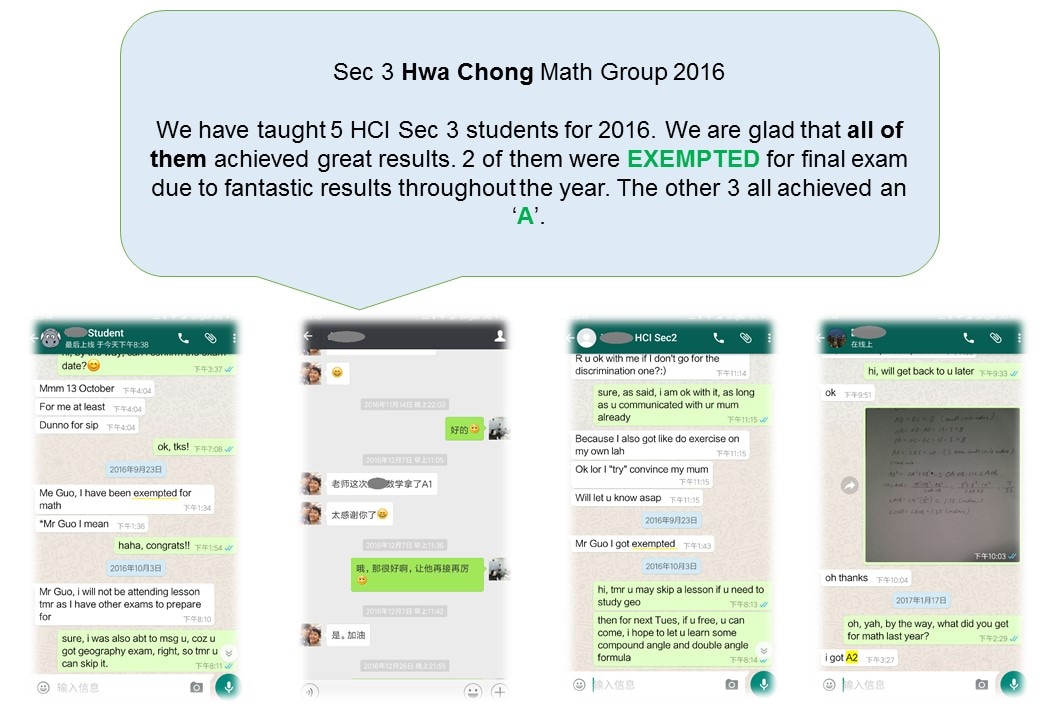
Here are some recent great improvements achieved by students, accompanied with evidences.
In order to protect student's personal information, only initials are shown. Original photoes are with MaxiMath and can be shown upon request.
|
See what students say about Mr Guo
|
|
Jill Ch., Hwa Chong Institution, scored perfect A in 2014 A level H2 Math. She improved from 'U' to 'A' in half a year.
Jiang G., Catholic JC, scored A in 2014 A level H2 Math
Abigail N., NanYang JC, scored A in 2014 A level H2 Math. She improved from 'U' to 'A' in one year.
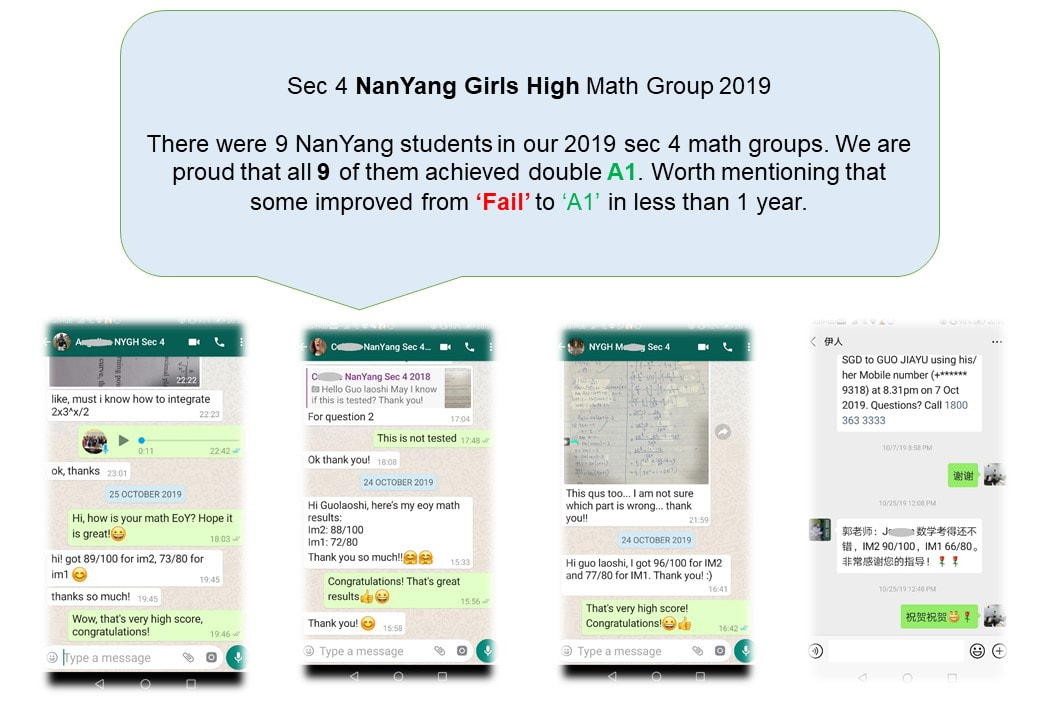
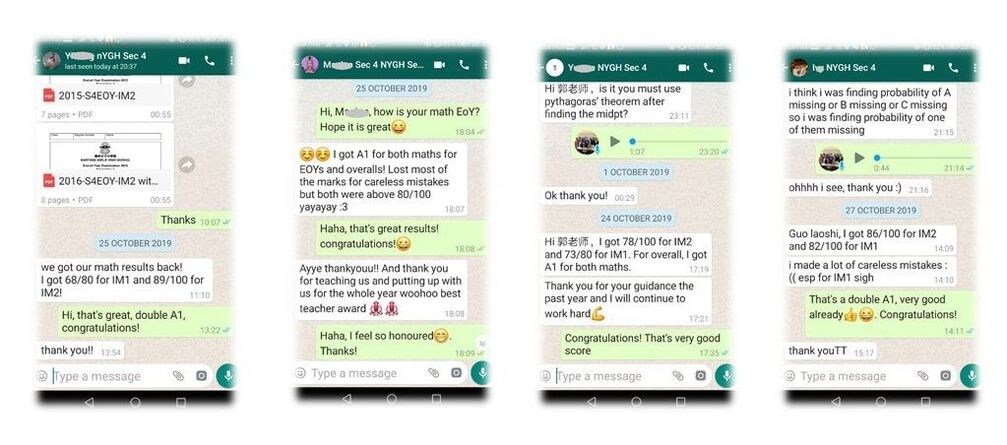
J. Ch., NanYang Girls' High, Sec 3, scored double A1 for her IM1
(E-Math) and IM2 (A-Math). She only obtained D7 at end of Sec 2 and had to retake her Math exam.
BEFORE -- Sec 2 EOY Math Score 46 Grade D7.
|
AFTER -- Sec 3 EOY IM1 (E-Math) Score 79/100 Grade A1.
|
AFTER -- Sec 3 EOY IM2 (A-Math) Score 88/100 Grade A1.
|
Ch.Y.Q, NanYang Girls' High, Sec 4, scored double A1 for her IM1
(E-Math) and IM2 (A-Math). She only obtained C5 at end of Sec 2 and had to retake her Math exam.
BEFORE -- Sec 2 EOY Math Grade C5.
|
AFTER -- Sec 4 EOY IM1 (E-Math) Score 81/100 Grade A1.
|
AFTER -- Sec 4 EOY IM2 (A-Math) Score 83/100 Grade A1.
|
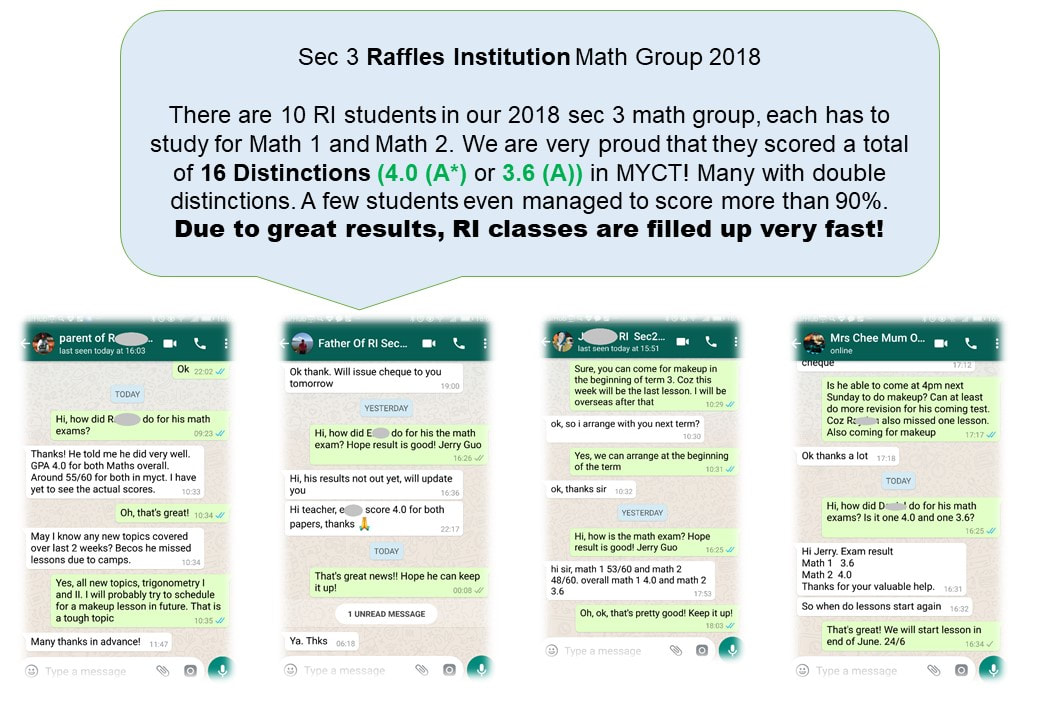
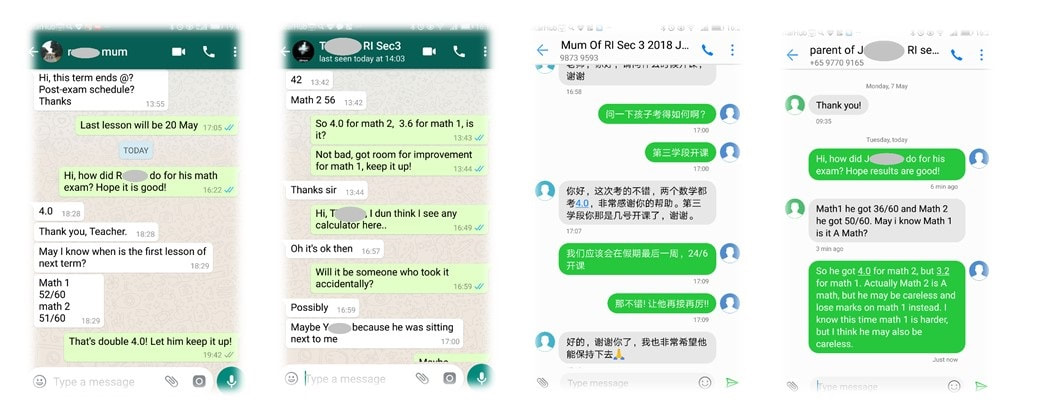
Se. M., Raffles Institution, Sec 3, scored double A* (GPA 4.0) for his IM1 (E-Math) and IM2 (A-Math).
IM1 score 95/100, Grade A*, GPA 4.0
|
IM2 score 84/100, Grade A*, GPA 4.0.
|
J.T., ACS, Sec 3, improved his A-Math from C6 to A1
BEFORE -- Mid Year Exam, Score 54/100. Grade C6.
|
AFTER -- EOY Exam, Score 97/120 = 81/100. Grade A1.
|
A. N., Catholic High, Sec 3, improved his A-Math from C5 to A1
BEFORE -- Mid Year Exam C5.
|
AFTER -- End of Year Exam A1
|
L.H.Q. , Beatty School, Sec 1, improved his Math from C6 to A2
Left -- Result BEFORE. Right -- Result AFTER
A. T., Tanjong Katong Girls', Sec 3, improved her A-Math
from 39 to 60 in just 3 months
BEFORE -- Mid Year Exam, Score 35/90 = 39/100, Grade F.
|
AFTER -- Mid Year Exam, Score 54/90 = 60/100, Grade B4
|
O. H., Raffles Institution, Sec 2, scored A (GPA 3.6) for his Math.
Math Score 75/100, Grade A, GPA 3.6
Timothy & MingPeng, Tao Nan School, P5, won NMOS Bronze medal after a mere 17 lessons. And subsequently a Silver medal in SMOPS. Both students have not recieved Math Olympiad training before.
